We recently implemented a procedure called bootstrap aggregating, or bagging, to increase the skills and the stability of our neural network models.
Bagging (Breiman 1996) works as follows: First training pairs, consisting of the data at the initial time and the forecast target of certain months (leadtime) later, are formed. The available training pairs are separated into a training set and a test set. The test set is reserved for testing only and not used for training. The training set is used to generate an ensemble of neural network models; each member of the ensemble is trained by only a subset of the training set. The subset is drawn at random with replacement from the training set. The subset has the same number of training pairs as the training set; some pairs in the training set appear more than once in the subset, and about 37% of the training pairs in the training set are absent in the subset. The final model output is the average of the outputs from all members of the ensemble.
The advantage of bagging is to reduce the variance, or instability of the neural network. The error surface of neural network training is full of local minima; trainings with different initial weights and training data are usually trapped in different local minima. These local minima reflect partly the fitting to the regularities of the data and partly the fitting to the noise in the data. Bagging tends to cancel the noise part as it varies among the ensemble members, and tends to retain the fitting to the regularities of the data.
The neural networks were trained with the NINO3.4 index (from http://nic.fb4.noaa.gov/data/cddb/), and the FSU monthly wind stress (Goldenberg and O'Brien 1981, from ftp://coaps.fsu.edu/pub/wind/pac). The gridded wind stress data were reduced to a few EOF modes. Before the EOF calculation, the wind stress data were first smoothed with one pass of a 1-2-1 filter in the zonal and meridional directions and in time, and detrended and de-seasoned by subtracting from a given month the average of the same calendar months of the previous four years. This pre-EOF processing is the same as that used in Lamont's coupled model (Cane et al. 1986) and in Tang (1995).
The neural networks in this forecast have 11 inputs and 5 hidden neurons. The NINO3.4 index, the 2nd and 3rd EOF time series of the wind stress of the initial month form the first 3 inputs. (The first EOF time series was not used because it is almost the same as the NINO3.4 index.) The same 3 variables of 2 months and 4 months before the initial month are also used as inputs. The last 2 inputs are the sin and cos of a 12-month period to simulate the annual cycle.
The ensemble in the bagging procedure has 30 members. For each leadtime, we produced 5 bagging neural networks, with 5 different test periods: 1963-1969, 1970-1977, 1978-1984, 1984-1990, and 1991-1996. Table 1 lists the skills for leadtimes of 3 months to 12 months, and for the 5 test periods. To show the improvement brought by bagging, we also lists in Table 2 the average of the test skills of the individual members of the ensemble.

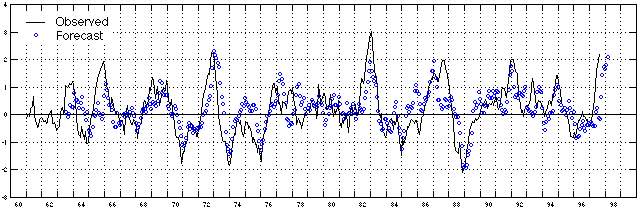
The above figure plots the model outputs of test periods, collected from the 5 runs of different test periods, against the observations. The leadtime is 6 months.
Table 1. The test correlation skills for different test periods
test period 3-month 6-month 9-month 12-month 1963-1969 0.85 0.67 0.56 0.35 1970-1976 0.91 0.78 0.55 0.31 1977-1983 0.81 0.70 0.58 0.47 1984-1990 0.90 0.83 0.69 0.46 1991-1996 0.91 0.81 0.59 0.25
Table 2. The average of the test skills of the individual members of the ensemble
test period 3-month 6-month 9-month 12-month 1963-1969 0.82 0.61 0.42 0.23 1970-1976 0.89 0.73 0.48 0.23 1977-1983 0.78 0.64 0.43 0.26 1984-1990 0.88 0.78 0.56 0.30 1991-1996 0.88 0.73 0.44 0.18
Breiman, L., 1997: Bagging predictions. Machine Learning, 24, 123-.
Cane, M.A., S.E. Zebiak and S. Dolan, 1986: Experimental forecasts of El Nino. Nature, 321, 827-832.
Goldenberg, S.B., and J.J. O'Brien, 1981: Time and space variability of tropical Pacific wind stress. Mon. Wea. Rev., 109, 1190-1207.
Tang, B., 1995: Periods of linear development of the ENSO cycle and POP forecast experiments. J. Climate, 8, 682-691.
Tangang, F.T., W.W. Hsieh and B. Tang, 1997: Forecasting the equatorial Pacific sea surface temperatures by neural network models. Climate Dynamics, 13, 135-147.
Tangang, F.T., B. Tang, W.W. Hsieh and A. Monahan, 1997: Forecasting ENSO events: a neural network appoach, J. Climate, accepted.
Tangang, F.T., W.W. Hsieh and , B. Tang, 1997: Forecasting regional sea surface temperatures in the tropical Pacific by neural network models, with wind stress and sea level pressure as predictors, J. Geophys. Res., submitted.